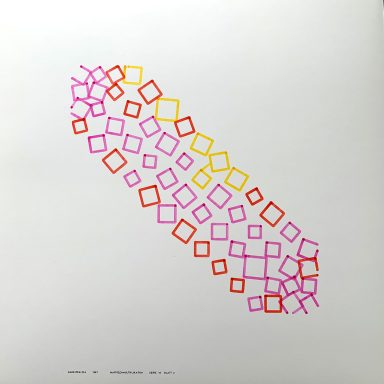
Matrizenmultiplikation (Matrix Multiplication)

Basic Information

Title: Matrizenmultiplikation (Matrix Multiplication)
Artist(s): Frieder Nake
Date Created: 1967
Framed Dimensions: 21.75 x 21.75 in.
Unframed Dimensions: 18.75 x 18.75 in.
Medium: plotter drawing in ink on paper
Inventory ID: Nake-1967-07A,B,C,D,E,F,G,H,I,J,K,L

Description

a portfolio of twelve plotter drawings, one colophon page, and one computer code print out in a custom made quad-fold portfolio

each drawing is signed, titled, and dated in machine ink
each drawing is signed, titled, and dated in graphite on the reverse of the paper

printed and published by Hansjörg Mayer

hardware: Telefunken-Rechner 4
output machine: Zuse Z64 Graphomat plotter

portfolio: 18.75 x 48″ open / 19 x 19″ closed
computer code printout: 24 x 15″
colophon page and plotter drawings: 18.75 x 18.75″

titles of artworks in visual order:
A. Serie 12 Blatt 1
B. Serie 19 Blatt 1
C. Serie 19 Blatt 2
D. Serie 12 Blatt 2
E. Serie 19 Blatt 3
F. Serie 19 Blatt 4
G. Serie 12 Blatt 3
H. Serie 19 Blatt 5
I. Serie 11 Blatt 1
J. Serie 12 Blatt 4
K. Serie 11 Blatt 2
L. Serie 11 Blatt 3

English translation of portfolio cover:
Frieder Nake
matrices
multiplications

edition hansjöerg mayer
stuttgart 1967
12 computer graphics and
1 program sheet
printed in 40 copies
26 of them in retail
signed and numbered
from a to z
this is the folder h

English translation of colophon page:
to the program matrix multiplication

The computer graphics in this folder are 3 of the series of the program matrix multiplication that were generated.

1. Computer graphics are two-dimensional visual aesthetic objects created in cooperation between humans and computers. In this case the human works together with the electronic computer system telefunken tr4 and the punched tape controlled drawing machine zuse z64. This cooperation works as follows: man invents a program that the computer should process. He still has certain freedoms. The barriers to these freedoms are set by people as fixed or variable in the program. They can be arbitrarily narrow or arbitrarily wide.
In the system I use, the computer delivers a punched tape as a result, in a certain code which contains graphics. The punched tape is processed by the automatic drawing machine. It is decoded and converted into the lines and colors of the graphic. This emergence process can be understood as a linguistic process.
First the program is created, i.e. a first text that has the character of a command, because it asks the computer to carry out certain prescribed actions. The computer fills in the blanks of the text at its own discretion. It then delivers a second text from the punched tape, which again has the character of a command.
For the drawing machine you have hardly any freedom left, namely only to use different colors and line widths. It submits the drawing as the final text. It no longer has any trace of an imperative nature, but rather passively faces the environment for perception and further processing.
What the framework of the program contributes to the graphics has deterministic character. What the random choices of the computer contribute to the graphics has a stochastic character.

2. Matrices are mathematical bundles that contain a finite set of numbers arranged in rows and columns so as to form a rectangular arrangement.

a11 a12 a13 a1n
a21 a22 a23 a2n

am1 am2 am3 amn

This example matrix has m rows, n columns, and nm numbers. Operations such as addition, subtraction, multiplication, and others can be preformed on matrices. In particular, one can compare a matrix with itself.
Multiply and get the matrix a to the power of 2.
Multiply this again by a and this again etc.
This way you get the powers: a to the power of 3, a to the power of 4, a to the power of 5, etc. a sequence of matrix powers.

3. The finite set of numbers in a matrix are all in a certain number range; an interval. If one divides this interval into sub-intervals in any way and assigns a character to each of the sub-intervals, then the mathematical matrix structure of numbers corresponds to a visual matrix structure of characters. This assignment of characters to numbers causes the visualization of a mathematical object, in other words, the concretization of an ideal object.

4. The series of sheets in this folder are part of an attempt to visualize a sequence of matrix powers. The aim is not to illustrate a mathematical process, i.e. to explain it in pictorial form. Rather, the mathematical process should be translated into a visual process, which can be viewed detached from the background of the mathematical process. It seems to me that it makes sense to use computers to hand over the tedious arithmetic work and to exploit the free imagination of the machine.
According to the character of the process, a large part of the information conveyed lies in the changes from sheet to sheet. The repertoire of symbols on which these sheets are based consists of squares of different colors, the size of which is chosen at random. Like the matrices used, the choice of the dimensions of the squares depends on the date and time at which the computer is working, i.e. completely beyond my manipulation.

5. At each stage of the process, i.e. each sheet of the series, the computer provides a series of measurements on the aesthetic object it creates. Terms of criteria on aesthetics are used for this. The following numerical values are obtained for each sheet: relative frequency, surprise value, and conspicuousness of each of the occurring signs. For definitions see h frank cybernetic analysis of subjective facts, publishing house fast – quickborn 1964. The computer also provides the average information per character and the overall information, namely on the level of the characters themselves and on a super-character level. By plotting these values for all the sheets in a series of charts, one gets an overview of how the stated aesthetic criteria change from sheet to sheet.
If you use the numerical values, you can discuss the sheets without having to pass judgment. In addition to the attempt to visualize a mathematical process, we have the attempt to mathematicize a visual process.

6. The series in this folder are only examples from the production of the matrix multiplication program. In this production there are any number of other series that would receive a very similar judgment as the ones presented here, and also any number of series with extremely different judgments. In this sense, not only the distribution of the characters on the sheets is random, but also the selection of the sheets from the overall ensemble.

For further information about this work see the Tate Museum collection